傅立叶级数(Fourier Series)和周期现象
作者:linuxer 发布于:2014-8-7 20:09 分类:基础学科
一、前言
如果你仔细观察,工作和生活中充满了周期现象:旁边linux driver工程师在调试audio driver的时候播放的1kHz的正弦信号,周末去公园游玩,游船推开水面的波纹,硬件工程师调试硬件电路的时候,示波器显示出来的晶振方波信号……
所谓周期现象具体包括时间上的周期现象和空间上的周期现象。1kHz的audio当然是时间上的周期信号,而水面的波形就是空间上的周期现象。对于空间上的周期现象,实际上就是一个pattern不断的重复。
对于一个普通的人,我们可以感知时间的流逝,也可以感知空间的变化(我们可以通过眼睛、耳朵、触觉等build in在身体上的sensor来感知时空中的周期现象),因此,周期现象对于我们来讲就像呼吸一样自然。然而,你是否愿意从另外一个侧面来感知世界?那个世界就是频域(frequency domain)的世界。描述时间上的周期现象我们使用频率(frequecy)这个词,也就是一秒重复的次数。
Can you feel frequency of the world?
二、信号的分解
在进入傅立叶级数之前,我们首先理解下面两个概念:
(1)分析(analysis)。也就是把一个复杂的信号(函数,后面的描述中我们不区分函数和信号这两个术语)分解成较为简单的成分(例如sin、cos函数等)。
(2)合成(synthesis)。通过简单的成分重新构造复杂的信号(函数)
在本章,我们首先了解矢量的分解,这个概念比较简单,比较好理解。之后进入函数的分解,也就是本文的核心了。
1、矢量的分解
一个二维矢量的分解我们参考下图中左边的那个图:
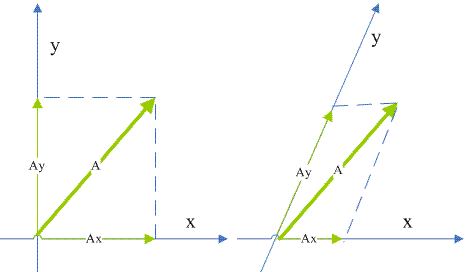
矢量A可以通过向x和y轴投影,将A分解成两个简单的矢量Ax和Ay,A可以是二维空间中的任意矢量,但是总是能分解成沿着x轴和y轴的两个简单的矢量。这种分解是唯一的吗?当然不是,上图中右边的矢量分解也是OK的,只不过坐标轴不是垂直的而已。
我们当然可以把事情变得更复杂,比如三维空间,当然,概念是一样的,只不过我们的坐标轴是x、y、z三个轴。一般的分解都是把坐标轴设定为两两垂直的,如果你愿意,不垂直也没有问题。推广到n维空间如何?当然可以,只不过n维空间没有直观的图形表示,需要依靠你的想像。
2、函数的分解
我们来研究周期为1的信号,也就是说f(t+1)=f(t)。我们对该函数进行分析,并试图将该信号分解成更简单的信号,这里我们sin和cos函数来进行分析。由于信号的周期是1,因此频率也是1,所以用于建模的信号就是sin(2π t)和cos(2π t)。
首先考虑信号:sin(2π t) + sin(4π t) + sin(6π t)+......
对于sin(4π t)这个函数,虽然他的频率是2,但是毫无疑问,每隔一秒,其pattern也是重复的(每隔0.5秒重复一次,实际上,每隔1秒其波形一定也是重复的)。我们将这些频率为1、2、3......的函数加在一起,得到的是一个频率为1的函数(每个函数有同样的特性:每隔1秒重复其波形,讲这些有同样性质的函数相加,其结果应该也是具备同样的特性)。
上面我们利用一个简单的周期为1的sin函数以及其各次谐波函数相加,人为的构建了一个周期为1的函数。这些函数还不够通用(例如t=0的时候,函数值都是0),能否创建更通用,但周期仍然是1的函数呢?调整各个谐波的幅度和相位,我们可以得到各种各样的更通用的函数。
OK,现在我们考虑相反的问题,是否任意一个频率为1(周期为1)的函数都可分解成各个频率成分(1、2、3......)的线性组合呢?如果这个命题成立,那么任意一个周期函数都可以分解成若干个简单的sin函数的和。这个概念和矢量分解没有什么不同,各个频率的sin函数就是n维空间中的n个坐标轴,函数在坐标轴上的投影就是该sin函数的幅度值。
3、矢量分解和函数分解
我们先看看点积(dot product)的概念。向量A(a1,a2)和向量B(b1,b2)的点积是
被积函数是f(t)乘以g(t)的共轭,之所以会出现共轭是因为f(t)和g(t)可能是复变函数。如果是实函数,那么其共轭就是函数本身(本来是不想出现共轭这样的概念,但是后面有复指函数,没有办法啊)。如果两个向量的点积等于0,那么我们就说这两个向量是正交的(orthogonal ,类似几何上的垂直),对于2维或者3维空间的向量,正交就是垂直。对于函数,如果f和g这两个函数的点积满足
我们再来看看2维空间的坐标系。两个向量(1,0)和(0,1)可以表示两个非常基础的向量(也就是传说中的标准正交基,standard orthogonal basis),这两个向量就象坐标轴一样,实际上任意的一个向量都可以分解成(1,0)和(0,1)的线性组合,或者反过来说,这两个向量的线性组合可以充满整个2维向量空间。对应函数空间,我们是否也能找到一组两两正交的函数呢?并且这组函数的线性组合可以充满整个函数空间。如果能找到,那么函数空间中的任意一个函数都可以分解成标准正交基的组合。其实这样的函数集有非常多,傅立叶级数只是选取了sin,cos或者复指函数作为标准正交基而已。
对于矢量,我们可以定义其长度。矢量A和自己进行点积运算就可以得到矢量长度的平方。长度的概念也可以引申到函数领域。如果||f||表示函数的长度或者函数的模,那么:
4、软件设计的分解
什么是知识?所谓知识,就是必须能应用到你的生活行为中方为知识。你能够背诵它,你能够推导它,都不能说明什么,只有理解之后并能够用来指导自己的工作和生活的那些才是真正的知识。当然,这里的生活当然说的不是去购物或者做饭,主要是应用到工程中。对于我们而言,就是分解的思想应用到软件设计中或者issue的修复中。
软件的设计过程就是把一个复杂的事情分解成一个一个简单的事情,然后逐个击破的过程。软件架构师做庖丁解牛的工作,而普通的程序员做简单的模块的相关工作。
三、从时域到频域
上面一段有点扯,我们先回到上文中的那个假设命题:任何复杂的频率为1(周期为1)的函数都表示为:
f(t) = 对于k=1~N上求和( Ak sin(2πkt +pk ) )
pk是各次谐波的相位,Ak是各次谐波的幅度。
首先,先简化问题,去掉相位,也就是说所有的谐波相位固定为0。这样各个谐波不能单纯的表示为sin函数,而是sin和cos的组合(也就是说相位 的信息体现在了sin和cos的幅度上)。这时候,我们有2N个坐标轴,N个是sin族函数,另外N个是cos族函数。函数投影到这些坐标轴上就可以知道函数在该坐标轴(谐波,sin或者cos函数)上的幅度(坐标值)。根据欧拉公式可以进一步简化,谐波表示为exp(2π ikt),i是虚数单位,k是谐波次数。
exp(2π ikt)=cos(2πkt) + i sin(2πkt)
使用幂指数(exponential)虽然好,但是谐波的次数从原来的0~n变成 -n~n,也就是说引入了负频率的概念。具体的公式是:
f(t) = 对于k=-N~N上求和( Ck exp(2π ikt) )
Ck就是傅立叶系数,表示各次谐波的幅度。
虽然表达式不一样,但是其本质是一样的,都是将周期为一的复杂的信号分解成各次谐波exp(2π ikt)的线性组合。
既然假设了上面的公式成立,那么Ck如何求?过程比较简单,对于m次谐波,利用代数的方法将其移到等式的左边,其他项移到等式的右边,同时乘 exp(-2π imt),然后对等式两边求一个周期上的积分。exp(2π ikt)这一组函数应该是函数空间(对应向量空间)的标准正交基(相互垂直的坐标轴),因此,当不同次谐波的积分应该等于0。这样Ck可以按照下面的公式计算:
Ck = 在0~1上求积分( exp(-2π ikt) f(t) )
虽然我们求出了Ck,但是是否真的适用于所有的信号?答案是否定的。在微积分课程中,我们学习到下面的知识:连续函数的和也是连续函数。在这样的背景下,一个周期为1,占空比为50%的开关信号是不可能用有限个连续的sin或者cos函数表示出来。我们可以追加一个问题:一个周期为1锯齿信号是连续的,是否可以用有限个连续的sin或者cos函数表示出来?答案也是否定的。在微积分课程中,我们学习到下面的知识:可微函数的和也是可微函数。锯齿信号虽然是连续的,但是不是可微的(一阶就不可微了)。只有足够平滑(任意阶可微)的函数才可以用有限个sin或者cos函数表示出来。对于那些不够平滑,甚至有不连续点的函数,需要引入无穷级数:
f(t) = 对于k=-∞~∞上求和( Ck exp(2π ikt) )
只要f(t)在一个周期内是一个有限能量信号,就可以保证上面的公式成立。当然,上面公式中的等号仅仅是意味在均方意义下,左右两边相等。由于引入了无穷项,因此需要考虑收敛性。关于收敛性,还是留给数学家吧。
最后再罗嗦一点关于投影的事情。矢量的分解需要计算其在坐标轴上的投影,矢量(a,b)在x轴(1,0)上的投影实际上就是计算他们的点积。我们可以来看傅立叶级数中的复指函数集合exp(2π ikt),这些函数集组成了函数空间中的一组标准正交基。而傅立叶系数Ck就是f(t)在标准正交基上的投影。因此Ck = <f(t), exp(2πikt)>。
四、后记
我的有些博文中有大量的数学公式,这是我的一个业余爱好。但是我的一个朋友告诉我:你写这些东西只能让你自己爽,当文章中出现第一个数学公式的时候,一般的读者已经放弃阅读了。本来我想用更通俗的语言来描述线性代数和泛函分析的一些基础概念:vector space、正交、function space、标准正交基什么的,但是看起来功力还是不够,特别是对于泛函分析,我基本上还是只理解皮毛。我想只有我深入理解这些东西的时候才能用大家都明白的语言描述出来,不过目前也只能这样了。
原创文章,转发请注明出处。蜗窝科技。http://www.wowotech.net/basic_subject/Fourier_Series.html
评论:
2014-11-06 11:11
exp(jwt)=cos(wt) + j sin(wt)
个人认为,信号处理的各种变换、公式、定理都源自欧拉公式,
但真心不知道公式是怎么来的,怎么理解?
2014-11-06 12:51
如果你用同样的方法来对cos(x) + j sin(x)进行运算,得到的结果和上面类似的。
实际的数学证明网上一大把,我只是用简单的语言描述之而已,这是我对欧拉公式的理解。
功能
最新评论
文章分类
随机文章
文章存档
- 2025年4月(5)
- 2024年2月(1)
- 2023年5月(1)
- 2022年10月(1)
- 2022年8月(1)
- 2022年6月(1)
- 2022年5月(1)
- 2022年4月(2)
- 2022年2月(2)
- 2021年12月(1)
- 2021年11月(5)
- 2021年7月(1)
- 2021年6月(1)
- 2021年5月(3)
- 2020年3月(3)
- 2020年2月(2)
- 2020年1月(3)
- 2019年12月(3)
- 2019年5月(4)
- 2019年3月(1)
- 2019年1月(3)
- 2018年12月(2)
- 2018年11月(1)
- 2018年10月(2)
- 2018年8月(1)
- 2018年6月(1)
- 2018年5月(1)
- 2018年4月(7)
- 2018年2月(4)
- 2018年1月(5)
- 2017年12月(2)
- 2017年11月(2)
- 2017年10月(1)
- 2017年9月(5)
- 2017年8月(4)
- 2017年7月(4)
- 2017年6月(3)
- 2017年5月(3)
- 2017年4月(1)
- 2017年3月(8)
- 2017年2月(6)
- 2017年1月(5)
- 2016年12月(6)
- 2016年11月(11)
- 2016年10月(9)
- 2016年9月(6)
- 2016年8月(9)
- 2016年7月(5)
- 2016年6月(8)
- 2016年5月(8)
- 2016年4月(7)
- 2016年3月(5)
- 2016年2月(5)
- 2016年1月(6)
- 2015年12月(6)
- 2015年11月(9)
- 2015年10月(9)
- 2015年9月(4)
- 2015年8月(3)
- 2015年7月(7)
- 2015年6月(3)
- 2015年5月(6)
- 2015年4月(9)
- 2015年3月(9)
- 2015年2月(6)
- 2015年1月(6)
- 2014年12月(17)
- 2014年11月(8)
- 2014年10月(9)
- 2014年9月(7)
- 2014年8月(12)
- 2014年7月(6)
- 2014年6月(6)
- 2014年5月(9)
- 2014年4月(9)
- 2014年3月(7)
- 2014年2月(3)
- 2014年1月(4)



2019-02-28 11:53